本文地址:http://sokoban.ws/blog/?p=2330
作者:杨超
这个月,2016年3月,Google 的 DeepMind 团队开发的围棋程序 AlphaGo 在韩国首都以 4:1 战胜世界冠军围棋九段李世石。早在近20年前,IBM 的国际象棋程序“深蓝”就已经战胜人类冠军。而围棋棋盘比较大,人们普遍认为人类对计算机程序的优势在围棋项目还可以保持比较长的时间。而这次 Google 团队的胜利,证明了其实开发一个战胜人类的下围棋程序并没有那么难,而是开发这样的程序没有太大的直接收益,哪怕是国际象棋和围棋这样就有悠久历史传统和广泛的群众基础和关注度的棋类。
围棋究竟有多难?我们拿它和推箱子来比较一下。恰好我刚刚完成了用三篇博文来介绍推箱子问题的计算复杂度:推箱子是PSPACE完全问题。
为了从计算复杂度方面和推箱子问题比较,我们需要准确地定义一下什么叫围棋问题。
虽然人们常说围棋的变化很多,但是无论变化有多少,终究是一个有限的数。所有有限步内能分出胜负的、没有隐藏信息、也没有运气成分的二人棋类游戏,一定有一方有必胜策略(或者必和策略)。打个比分说,19路围棋按照中国的贴目规则也许是先手有必胜策略。那么我们所说的围棋问题,就是对于任意的n x n棋盘上下的围棋,如何设计一个算法来确定究竟是先手必胜还是后手必胜?或者等价地说,先手究竟有没有必胜策略?(即这是一个回答“是”或者“否”的问题)通常的19路棋盘围棋是围棋问题的一个实例。要回答这个问题,除了穷举所有的对弈变化之外,人们暂时还没能找到其它规律来判断谁有必胜策略。对围棋而言,穷举所需要的时间随着棋盘 n 的增大,是成指数增长的。事实上,已经有文献证明,按日本规则,围棋问题是EXPTIME完全问题(见[1,2],该文章作者猜测,若按中国规则,围棋问题可能更难,成为指数空间完全问题)。也就是说,在指数时间可解的问题里面,围棋问题是最困难的其中一个。除了围棋,其它一些棋类问题如国际象棋、西洋跳棋(checkers)都被证明是EXPTIME完全问题。其中8×8棋盘的西洋跳棋在使用计算机花了近20年的穷举计算后,在2007年被证明双方都采取完美策略一定是和棋。
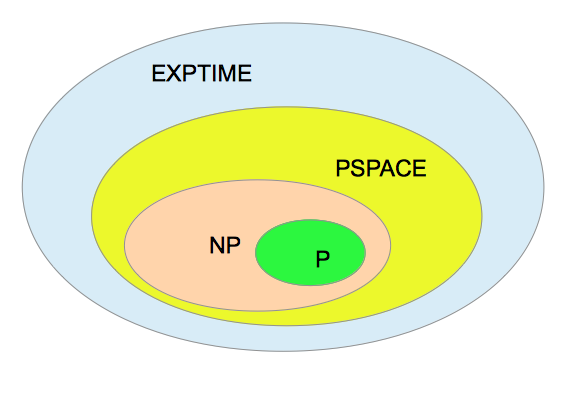
所以,从计算复杂度来看,包括围棋在内的许多棋类游戏比推箱子要难一个层次。计算复杂度的几个概念(EXPTIME、PSPACE、NP、P)的关系可用下图表示。虽然还没有从理论上严格证明,但是一般认为,从内到外,这四类问题的计算复杂度是严格地越来越难。
更有甚者,围棋问题的一些子问题,如征子能否成功问题在文献中被证明是PSPACE完全问题[3]。而围棋残局收官问题,则是PSPACE难的[4]。也就是说围棋问题的某些子问题就已经和推箱子问题一样难了。
那么,为什么比推箱子更难的围棋都已经开发出能战胜人类的程序,但是比围棋还容易一些的推箱子,我们却没有看到优秀的推箱子求解程序能够解出较大的、箱子数目较多的关卡呢?我想主要有以下这么一些因素。
首先,开发推箱子求解程序比开发下围棋程序更加无利可图。目前看到的一些求解程序基本都是个人单打独斗编写的,运行在个人电脑上,而且都是作为业余兴趣进行的。尚未看到有软件类企业或者研究团队投入较大资源来开发。作为对比,Google的AlphaGo程序投入了至少20人的开发团队,和李世石对战时动用了上千个CPU和GPU同时计算。
其次,AlphaGo虽然战胜了人类,但是并没有回答我们前面所定义的围棋问题,也就是说并不知道是否先手必胜。战胜人类并不需要穷遍所有变化,比判断19路围棋谁有必胜策略稍微容易一些。而一个推箱子关卡求解程序从某种意义上必须回答出推箱子问题,一般来说,必须穷遍所有路经才能判断一个关卡无解。而找到一个答案,除了穷举剪枝之外也还没有见到有人提出新的算法思路。
比较令人好奇的是,如果投入更多的人力和计算机运算资源,计算机求解推箱子能达到一个什么样的水平呢?能解出多大的关卡?解大关卡能比人解得更快吗?
第83期推箱子比赛,我们也借着这个机会,由麦英兄设计了一关AlphaGo关卡。这一关计算机能解出来吗?
[参考文献]
1. J. M. Robson, The complexity of Go, Proc. IFIP (1983) 413-417.
2. J. M. Robson, Combinatorial games with exponential space complete decision problems, Proc. Mathematical Foundations of Computer Science, Springer-Verlag, LNCS 176, 1984, pp. 498-506
3. M. Crasmaru and J. Tromp, Ladders are PSPACE-complete, Proc. 2nd Int. Conf. Computers and Games, Springer-Verlag, LNCS 2063, 2000, pp. 241-249
4. D. Wolfe, Go Endgames Are PSPACE-Hard, More Games of No Chances, MSRI Publications, Volume 42, 2002, pp. 125-136