作者:杨超
本文地址:http://sokoban.ws/blog/?p=843
在博文《推箱子游戏的一个箱子推动路径搜索算法》中,我介绍了推箱子游戏如何用鼠标双击或拖放来进行推箱子操作。我知道的大概有十多个甚至二十多个推箱子软件都实现了这一功能。最近,anian告诉我,他通过用20603兄的《一箭十万》关卡测试了多个推箱子软件,发现《YSokoban》的速度最快,点击箱子,瞬间程序就给出了所有能被推到的格子的提示。而我编写的《SokoPlayer HTML5》则需要约2秒。经过和anian兄的讨论,我们改进了算法,大幅度提高的效率,使得《SokoPlayer HTML5》也能瞬间给出提示(约3毫秒)。下面简单介绍一下我们如何作出改进的。
在一个箱子推动路径搜索过程中,要反复判断人是否能从箱子的一侧自由移动(即不推动箱子情况下)到箱子的另一侧。这个不难判断,用简单的广度和深度优先搜索都能在线性时间内得到答案。但是箱子推动过程中,箱子位置在变化,要在不同的位置都作出判断。假设涉及到的格子有n个,每判断一次要O(n)时间,但箱子最多也可能出现在n个不同的格子,要做n次这样的判断,所以总的时间复杂度是O(n^2)。当关卡比较大时,如《一箭十万》是50×50的关卡,不算墙体,格子也上千,导致计算时间比较长。
后来,我们发现判断各种位置下人能否从箱子一侧自由移动到另一侧,可以用一个线性时间算法完成。这可以用图论里的割点(Cut Vertex)和块(Block)的理论和算法来帮助我们。举一个具体的例子来说明什么是割点和块。割点把关卡区域分割成不连通的小区域,称为块。下图关卡中,黄色格子为割点,共有10个块,分别用数字1到10标记。
我们若能把推箱子地图所对应的图中的割点和块全部标记出来,那么回答人能否从一侧移动到另一侧就很简单了。可以用这两步来判断:(1)先看箱子是否在一个 割点上。若不是割点,则人一定能从箱子一侧移动到任意的另一侧。若是割点,则还要进行第2步判断。(2)看该箱子这两侧的格子是否属于同一个块。若是,则 能移动。否则不行。
如上图中,若箱子在割点G6位置,人能从箱子左侧(F6)移动到上侧(G5),因为属于同一个块3号。但不能从左侧(F6)移动到右侧(H6)。又若箱子在H4位置,由于H4不是割点,人可以从一侧移动到任意的另一侧。
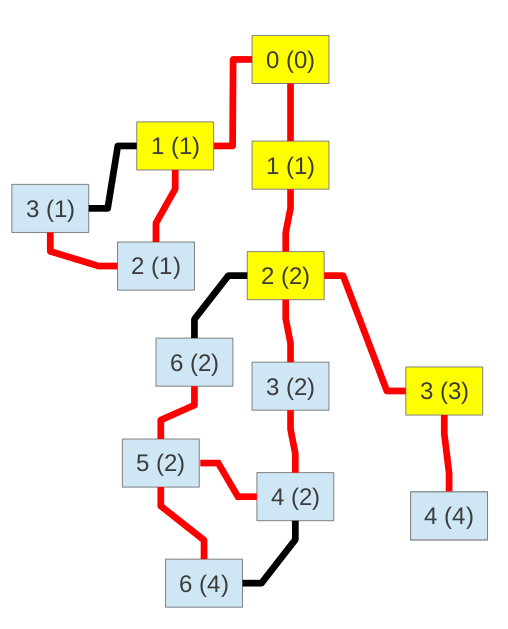
标记图的所有割点和块,有一个线性时间算法。这是一个基于深度优先搜索(Depth First Search)的算法。在深度优先搜索过程中,对每个结点记录两个参数。一个是结点的深度depth,另一个是结点的低位数(low point)。一个结点v的低位数是这样计算的,取下面三者的最小值:(a)v自身的深度,(b)v的所有邻点(DFS树中的父结点除外)的深度,(c)DFS树中v的所有子结点的低位数。
在实现中,通常用递归函数来进行深度优先搜索,于是计算低位数可以这样处理。每发现一个新结点v时,把低位数初始为该结点的深度(即a)。对v的每个邻点,若是父结点,不管;若是父结点以外的已访问结点,且若该结点的深度较当前的低位数小,重新赋值v的低位数为该结点的深度(即b);若是未访问结点,那么找到了一个子结点,于是递归调用搜索函数进行下一层搜索,返回时,若该子结点的低位数较小,则用它的更新v的低位数(即c)。
下面两幅图给出了一个例子,给出其DFS树(红色边),每个结点的深度和低位数。括号内为低位数,黄色结点为割点。
有了深度和低位数,如何判断割点和块呢?
对于割点,判断条件很简单,若结点v有某一个子结点的低位数大于等于v的深度,则v是割点。
搜索的根结点比较特殊,它是割点的条件是在DFS树中有至少两个子结点。
对于块的标记可以按如下方法实现。首先注意到割点同时属于多个块,其他点则恰属于一个块。在深度搜索过程中,每从一个子结点返回,并且由子结点判断出其父结点v是割点时,就意味着找到一个新的块了。此时,把v及其所有子孙都标记为同一个块。标记之后,在DFS树中,把v的所有子孙删掉,但保留v。这样v的子孙就不会被重复标记。而v是割点,还可能属于另外一个块。
以上文的图为例。2(2)是个割点,从子结点3(2)返回是能判断出来,同时能发现一个块。而从子结点3(3)返回时也发现2(2)是割点,于是2(2)在另外一个块中也被标记了。
[后两个图用LibreOffice Draw制作]
2013年12月22日补充:关于寻找割点算法,可参看用深度优先搜索(DFS)确定图的割点。



Pingback: [坑]POI补完计划#1 | qiancl