本文地址:http://sokoban.ws/blog/?p=2254
作者:杨超
本文是两篇博文《 一系列具有递归关系和指数长度答案的推箱子关卡》 和《 判断推箱子关卡是否有解的多项式空间的算法》 的续篇。这三篇博文构成推箱子与PSPACE问题三部曲。
一、什么是PSPACE完全问题(PSPACE-complete problems)
前两篇文章已经提过,PSPACE问题指的是:相对于实例(instance)的大小,存在多项式空间算法的判断性问题(decision problem)。
而PSPACE完全问题是PSPACE问题中最困难的一类。即一个问题A能够被称为PSPACE完全问题,如果问题A满足:对任何其他的PSPACE问题B,都存在一个多项式时间的方法把B的实例转化成A的实例,使得这两个实例在这两个问题中有相同的答案(都是“是”或者都是“否”)。由此定义,只要能给出某个PSPACE完全问题的快速算法,那么这个算法就可以用来解决所有的PSPACE问题。
我们这里所说的推箱子问题(SOKOBAN),指的是给出一个推箱子关卡(即实例),如何判断这个关卡是否有解。
无论从实践到理论,都有证据表明推箱子是非常困难的。
实践中,我们举办了好几年的MF8推箱子网络比赛,尚未见到有人或者组织能够用计算机快速解出我们的比赛主关。
在计算复杂性理论中,推箱子问题也被证明是一个PSPACE完全问题。本文的目的就是简单介绍一下这些证明。要证明推箱子问题(或者其他问题)是PSPACE完全问题,要论证两个方面:
一是推箱子首先是PSPACE问题。因为存在很多问题,其难度甚至超出PSPACE的范围,我们需要说明推箱子没有超出这个范围。这一点的证明较为容易,已经在三部曲的第二篇文中说过了。
二是证明推箱子是PSPACE问题里面最难的。这又有两种常用的方法,第一种方法是按照定义,描述一种方案把任何一个PSPACE问题的实例转化为推箱子实例。第二种方法就是,描述一种方案,把某一个已经被证明的PSPACE完全问题的每个实例转化成推箱子的实例。
无论是用那种方法证明,其技术性都是比较高的,比较依赖于巧妙的构思。
二、PSPACE完全问题的例子
已经有许许多多的问题被证明是PSPACE完全问题。这些问题可以被用来证明其他问题也是PSPACE完全问题。这里介绍两个比较有代表性的。
第一个是TQBF问题(True Quantified Boolean Formula)。这个问题的一个实例就是一个每个变量都带有量词(存在、任意)的布尔逻辑公式。公式中的每个变量只能取值“真”或者“假”。
如:(任意x)(存在y)(存在z) ((x或者y)并且z)
我们需要判断这样的一个公式是否总是“真”的。
第二个是LBA问题,即线性空间自动机(Linear Bounded Automata)。这个问题的一个实例是:给出一个线性空间自动机和一个输入,该自动机是否接受该输入。
这个问题的PSPACE完全性证明非常简单。因此利用此问题证明推箱子问题是PSPACE完全问题,和直接用定义证明推箱子问题是PSPACE完全问题,几乎没有多大区别。
除此之外,推箱子和滑块类游戏也是PSPACE完全问题的有趣例子。
三、推箱子是PSPACE完全问题
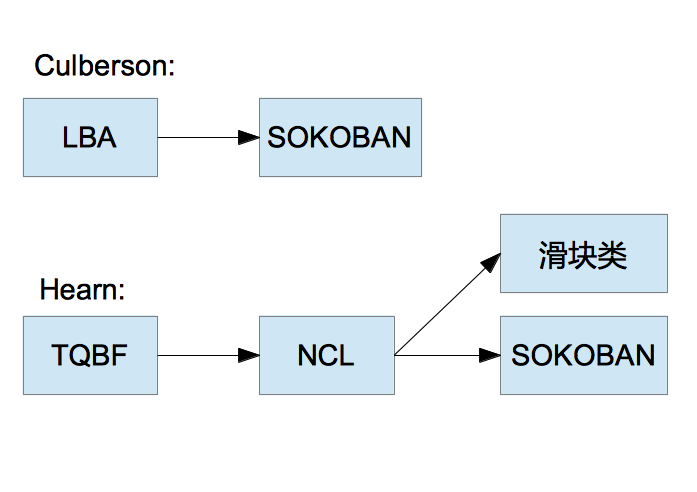
Dorit Dor和Uri Zwick在1996年写文章[1]研究了推箱子问题的计算复杂度,但未能证明推箱子是PSPACE完全的。加拿大阿尔伯特大学的Joseph C. Culberson看到该文后,在1997年就证明了推箱子是PSPACE完全问题[2]。
Culberson的证明方法是把LBA问题的实例转化为推箱子问题的实例。为此,他利用推箱子的规则设计了一些巧妙的局部关卡模块。这些模块限定了推箱子中的人为了过关,只能按照规定的路线走。把这些不同功能的模块拼接起来,通过人的行走路径,可以模拟图灵机(即自动机)的运行。这样任何一个LBA问题的实例就能转换为一个推箱子关卡。LBA问题的实例有肯定的回答当且仅当相应的推箱子关卡有解。
后来,在2005年前后,麻省理工大学的博士生Robert A. Hearn又给出了推箱子是PSPACE完全问题的另一种的证明方法[3,4]。Hearn先定义了一种抽象游戏NCL(Nondeterministic Constraint Logic,Hearn称之为一种计算模型)。通过把TQBF的每个实例转化为NCL的实例,Hearn证明了NCL问题也是PSPACE完全问题。Hearn定义的这个新问题NCL问题有一个好处就是,通过它来证明包括推箱子、滑块类在内的一些益智游戏是PSPACE完全问题,相对来说显得比较简单和清晰。
然后,Hearn把NCL的每个实例转化为推箱子的实例。在这个过程中,Hearn也是设计了一些具有不同功能的推箱子局部关卡模块。和Culberson的证明不同的是,Hearn的模块中,主要利用推箱子规则,使得一些箱子只能要么处于目标点,要么只能偏离目标点一格,这样完美地模拟了NCL游戏中的核心要素:0和1两种状态。并且,这种转化同样保证了NCL的实例有解当且仅当相应的推箱子实例(关卡)有解。
下图示意两种证明的总体思路的区别。
从实例的转化设计的细节上,Culberson主要利用人的行走路线模拟图灵机的运行。Hearn主要利用箱子的状态来模拟0、1两种状态,转化得到的关卡对人来说是“开放”的,可以随时访问任何一个箱子,不存在行走路径的限制。两者都用到了推箱子的某些特殊局部构造。
[参考文献]
1. Dorit Dor, Uri Zwick. SOKOBAN and other motion planning problems. Computational Geometry 13 (1999) 215-228 (submitted in 1996)
2. Joseph C. Culberson. Sokoban is PSPACE-complete. Technical Report TR 97-02 of Dept. of Computing Science, The University of Alberta. April 1997.
3. Robert A. Hearn, Erik D. Demaine. PSPACE-completeness of sliding-block puzzles and other problems through the nondeterministic constraint logic model of computation. Theoretical Computer Science 343 (2005) 72-96.
4. Robert A. Hearn, Games, Puzzles, and Computation. PhD Thesis of MIT. June 2006.
[修改说明]
2016年4月16日,增加对Hearn方法转换得到的关卡的特点描述。