作者:杨超
本文地址:http://sokoban.ws/blog/?p=630
之前写过一篇博文介绍了一系列具有递归关系和指数长度答案的推箱子关卡。本文给出判断推箱子关卡是否有解的多项式空间的算法。这两篇博文结合起来,可以对计算复杂性理论里面的PSPACE问题的概念有比较直观的理解。推箱子游戏是一个非常好的PSPACE问题的例子。
一、P, NP和PSPACE
先定义推箱子问题。本文中说的推箱子问题,是指如下的一个判断性的问题:给出一个推箱子关卡,这个关卡是否有解?注意这里只判断是否有解,也就是说只要回答“是“或“否“,如果回答“是“,也不需要给出一个具体可行的lurd答案。
判断一个推箱子关卡是否有解,是一个PSPACE完全(PSPACE-complete)问题。PSPACE-complete问题是计算复杂性理论里面的一个术语。PSPACE-complete 所讨论的是推箱子问题的空间复杂度。简单地说,空间就可以理解为计算机的内存。我们假设一个推箱子关卡宽度为w,高度为h,则我们称这个推箱子关卡的大小为n=w*h。显然,一个关卡越大,我们用程序去计算关卡是否可解时,需要的内存就越多。PSPACE-complete 有两层意思。第一层意思是推箱子问题存在多项式空间的算法,也就是说存在一个算法A,这个算法对大小为n的推箱子关卡,最多使用$ n^k $(k是某一个与关卡无关的常数)的大小的内存就能回答出这个关卡是否可解。当然,所用的时间没有限定。第二层意思是推箱子问题是所有多项式空间可解的问题里面最难的一类。PSPACE表示所有多项式空间可解问题的全体,PSPACE-complete是PSPACE 的一个子集,是里面最难的那些问题的全体。这里“最难“是有严格的数学定义的,在此我们直观地认为从空间复杂度考虑最难就可以了。
计算复杂性理论的完整的理论体系建立于20世纪的70年代(1970年代)。而推箱子最早被证明是PSPACE-complete问题是在上世纪90年代末。就像我们前面解释的那样,证明推箱子问题是PSPACE-complete问题有两个要点。一是要说明推箱子是多项式空间可解的。二就是说明推箱子问题是多项式可空间可解问题里面最难的。其中第一点比较容易,本文的目的是给出一个判断推箱子关卡是否有解的多项式空间的算法。注意,这个算法只是理论上有意义,不适宜用来实际求解。在实践中,大多推箱子求解程序使用大量的内存,往往是随推箱子关卡大小呈指数增长。
在具体讨论算法之前,先说些题外话。前些年,媒体曾热炒过“庞加莱猜想”,这是Clay数学研究所(Clay Mathematics Institute)于2000年悬赏100万美元的七个尚未解决的数学问题之一,每个100万美元。其中“庞加莱猜想”最近已经被解决了。2010年,这个百万大奖授予俄罗斯数学家佩雷尔曼(Grigoriy Perelman)。但佩雷尔曼拒绝接受这个奖项和奖金。 在其他六个尚未解决的价值百万美元的问题中,有一个是属于理论计算机科学里面的问题,更具体地说是关于计算复杂性理论的问题:即 P vs NP问题。
我们用P来表示所有能用多项式时间(注意是时间,不是空间,区别于PSPACE)算法解决的判断问题全体。用NP表示所有所有能用“非确定性(Non-deterministic)”多项式时间算法的判断问题全体。可以证明,任何一个P问题都一定是NP问题,也就是说P是NP的子集。但是现在尚未确定的是,究竟P是NP的真子集,还是P=NP?这就是所谓的P vs NP问题,七个百万问题之一。
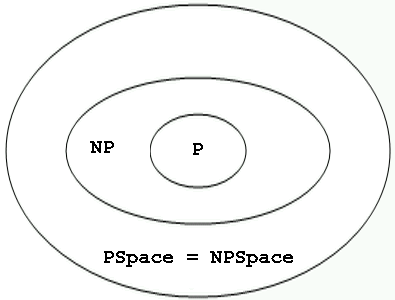
P和 NP都是从时间复杂度上考虑的,而PSPACE是从空间复杂度上考虑的。大家很自然会问,有没有NPSPACE问题?也就是说是否有“非确定性“多项式空间算法问题的全体呢?有的。但是作为著名的Savitch定理的一个推论,可以证明PSPACE=NPSPACE。即两者实际上是同一个集合,因此一般只提PSPACE。
Savitch定理是由Walter Savitch 于1970年证明的。我搜索了一下他的主页,发现他主页(http://cseweb.ucsd.edu/users/savitch/) 上照片似乎是在中国照的,大家可以去看看。这里提到Savitch定理的一个重要原因是下面介绍的算法是基于Savitch定理(参看[1])的证明设计的。
可以证明,凡NP问题都是PSPACE问题,NP是PSPACE的子集。那么究竟NP是PSPACE的真子集,还是NP=PSPACE?这也是一个悬而未决的问题。多数数学家和理论计算机学家都倾向于认为P,NP和PSPACE三者,前一个都是后一个的真子集,也就是可用下图示意:
二、判断推箱子关卡是否有解的多项式空间的算法
下面开始讨论算法。
我们知道一个大小为n的关卡,实际有效的格子实际上是小于n的,但我们不妨设就是n。每个格子要么是箱子,要么是人,要么什么也没有,所以所能形成的不同的局面不会超过$ 3^n $种(事实上$ 3^n $高估了所有可能的局面数,但从数量级上是基本一致的),其中有一个局面是初始局面,有一个是目标局面。所以,如果一个关卡是可解的,一定在$ 3^n $步内解出来,如果$ 3^n $步内不可解,这个关卡就是不可解了。并且我们也知道存在关卡,其解法的步数和关卡大小n是成指数函数关系,在博文《一系列具有递归关系和指数长度答案的推箱子关卡》中已经给出了例子。
一种直观的想法是用深度优先搜索(Depth-First Search)去穷尽所有$ 3^n $步以内的解法。但是这种算法需要用到一个后入先出的队列,这个队列的长度在极端情况下有可能是n的指数函数,这就超出了只用到关于n的多项式大小的空间的限制,就不是一个多项式空间算法了。
于是我们考虑一个基于二分法的递归算法去解决这个问题。
定义Savitch算法如下(姑且称之为Savitch算法吧,因为它是基于Savitch定理的证明,但文献中我没有看到有这样提法的)。
Savitch(c1,c2,t)
输入:初始局面c1,目标局面c2, 步数 t (初始局面和目标局面均为大小为n的关卡)
输出:若能在t步内由局面c1变换到局面c2,返回“是“,否则返回“否“
1,若t==1,能直接判断,返回“是“或者“否“。
1.1若c1==c2,返回“是“
1.2若c1!=c2,但能一步从c1变到c2,返回“是“
1.3其他情况,返回“否“
2,若t>1执行下面步骤。
3,对每个所有可能的中间局面cm
3.1递归调用 Savitch(c1,cm, [t/2])
3.2递归调用Savitch(cm,c2, [t/2]),(若t为奇数时,3.2调用Savitch(cm,c2,[t/2]+1) )
3.3若3.1和3.2均返回“是“,则直接返回“是“
4,若遍历了所有中间局面cm,3.3都没有返回,则返回“否“
对于一个大小为n的推箱子关卡,我们这样调用算法Savitch(c1,c2, $ 3^n $),则返回值就是我们想要的答案。下面说明一下算法只用了多项式空间。
每一层迭代,我们需要分配新的内存空间给c1,c2,t和cm,所以用的的空间不超过4n。那么最多迭代多少次呢?每迭代一次,步长除以2,所以最多经过 $ \log_2 3^n = (\log_2 3) n $次迭代,步长小于1,直接返回。所以,任一时刻,算法所用到的空间不会超过 $ (\log_2 3) n \cdot 4 n = (4\log_2 3) n^2$,这是关于n的一个2次多项式。所以这是一个多项式空间算法。
注:算法第3步遍历所有中间局面cm时,可按照局面的某种自然的字典排序去遍历,几乎不需要额外空间。
【参考文献】
[1] Sipser, Michael (1997), “Section 8.1: Savitch’s Theorem”, Introduction to the Theory of Computation, PWS Publishing, pp. 279–281
写于2011年1月,2012年8月26日修改